先上图：

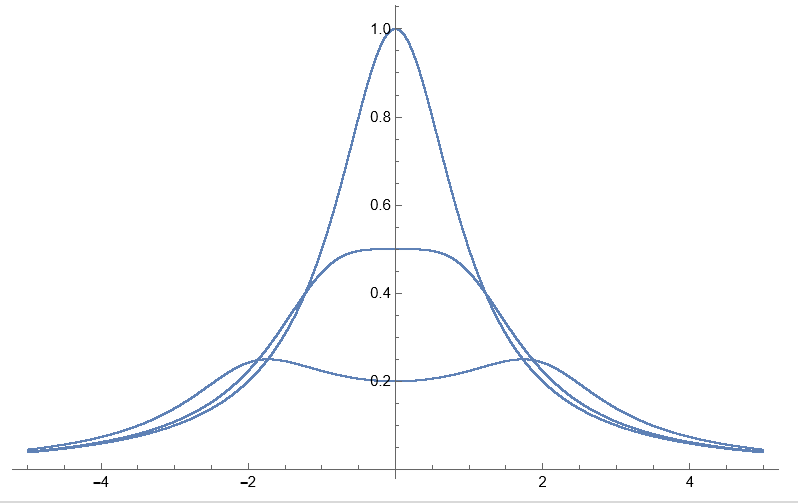
纵轴为$K$,横轴为$\xi=Q_L \frac{2\Delta f}{f_0}$，当$\xi _ 0 = 0,1,2$ 时的函数图像。
根据$|\frac{K_V}{K_{V0}}| = \frac{1}{\sqrt{1+(\frac{2Q_L\Delta f}{f_0})^2}}=\frac{1}{1+\xi ^2}$

mma代码如下：

ClearAll;
x = Range[-5, 5, 0.0001];
xx = 1/Sqrt[1 + x^2];
xx = xx^2;
data = Transpose[{x, xx}];
x2 = x + 1；
 xx2 = 1/Sqrt[1 + x2^2]；
 x3 = x - 1；
 xx3 = 1/Sqrt[1 + x3^2]；
 d2 = xx2*xx3
data2 = Transpose[{x, d2}];
x4 = x + 2；
 xx4 = 1/Sqrt[1 + x4^2]；
 x5 = x - 2；
 xx5 = 1/Sqrt[1 + x5^2]；
 d3 = xx4*xx5;
data3 = Transpose[{x, d3}];
Show[ListPlot[data], ListPlot[data2], ListPlot[data3]]