线性最小二乘问题

声明，如果有看到这个作业的，请遵循文章末尾连接中的知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议
属实是给我做吐了，只能结合各种工具慢慢来搞了）

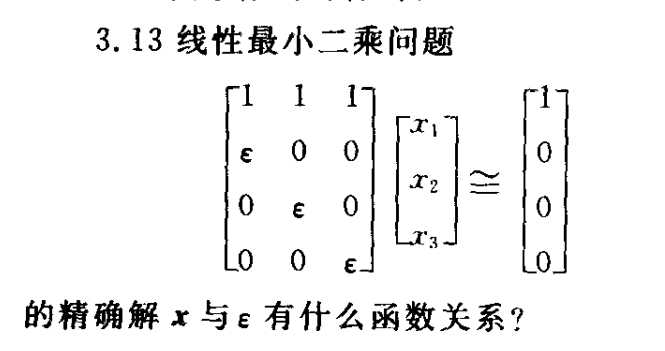
首先对于这个最小二乘问题，很明显，他是一个正规方程即矩阵A满秩，那么有 $A^TAx=A^Tb$ 与最小二乘问题 $Ax\cong b$ 同解，那么我们将上述最小二乘问题可以转化为

$\begin{pmatrix} 1+\varepsilon ^2&1&1 \\ 1&1+\varepsilon^2 &1\\ 1&1&1+\varepsilon^2\\ \end{pmatrix} \begin{pmatrix} x_1\\ x_2\\ x_3\\ \end{pmatrix}= \begin{pmatrix} 1\\ 1\\ 1\\ \end{pmatrix}$

得到x1,x2,x3的精确解为

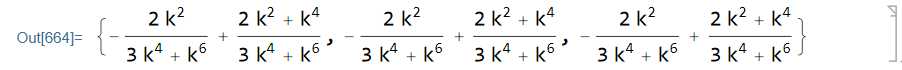
其中 $k=\varepsilon$
很容易看出，当 $\varepsilon$ 趋近于0的时候，最小二乘问题的解为 $x_1,x_2,x_3=\frac{1}{3},\frac{1}{3},\frac{1}{3}$
下面给出书上所有计算方案的实现：
注：解线性方程组使用全选主元的高斯消元法进行，代码如下

#include <stdio.h>
#include <cmath>
#include <cstdlib>
#include <iostream>
using namespace std;
#define N 100
const float eps = 0.0000001;
double b[N], x[N];
float r[N];
float a[N][N];
double A[N][N];
float ans[N];
int n;
int selectFull(int x)
{
    int px = x, py = x;
    for (int i = x; i <= n; i++)
        for (int j = x; j <= n; j++)
            if (fabs(a[i][j]) > fabs(a[px][py]))
            {
                px = i;
                py = j;
            }
    if (px != x || py != x)
    {
        for (int i = x; i <= n + 1; i++)
            swap(a[px][i], a[x][i]);
        for (int i = 1; i <= n; i++)
            swap(a[i][py], a[i][x]);
    }
    return 0;
}
int Gauss()
{
    float t;
    for (int i = 1; i <= n; i++)
    {
        selectFull(i);
        if (fabs(a[i][i]) <= eps)
        {
            printf("No Answers\n");
            return 0;
        }
        for (int j = i + 1; j <= n; j++)
        {
            if (fabs(a[j][i]) > eps)
            {
                t = a[i][i] / a[j][i];
                for (int k = i; k <= n + 1; k++)
                    a[j][k] = a[j][k] * t - a[i][k];
            }
        }
    }
    for (int i = n; i; i--)
    {
        for (int j = i + 1; j <= n; j++)
        {
            a[i][n + 1] -= a[i][j] * a[j][n + 1];
        }
        a[i][n + 1] /= a[i][i];
    }
    return 0;
}

int main()
{
    scanf_s("%d", &n);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n + 1; j++)
        {
            cin >> a[i][j];
            A[i][j] = a[i][j];
        }
    Gauss();
    for (int i = 1; i <= n; i++)
        printf("%f\n", a[i][n + 1]);
    return 0;
}

(a)正规方程组

Complex A;
    A.m = 4;
    A.n = 3;
    A.a[1][1] = A.a[1][2] = A.a[1][3] = 1;
    A.a[2][1] = esp; A.a[2][2] = 0; A.a[2][3] = 0;
    A.a[3][1] = 0; A.a[3][2] = esp; A.a[3][3] = 0;
    A.a[4][1] = 0; A.a[4][2] = 0; A.a[4][3] = esp;

    Complex b;
    b.m = 4;
    b.n = 1;
    b.a[1][1] = 1; b.a[2][1] = 0; b.a[3][1] = 0; b.a[4][1] = 0;
    Complex At = !A;
    Complex c1 = At * A;
    cout << c1;
    Complex c2 = At * b;
    cout << c2;

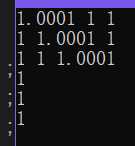
计算得到的 $A^TA$ 在eps>=0.01时会对结果产生影响，结果如下图所示:

代入高斯消元中可以发现结果出现误差：

(b)增广方程组

将最小二乘问题转化为增广方程组形式：

$\begin{pmatrix} I&A \\ A^T&0 \\ \end{pmatrix} \begin{pmatrix} r\\ x\\ \end{pmatrix}= \begin{pmatrix} b\\ 0\\ \end{pmatrix}$

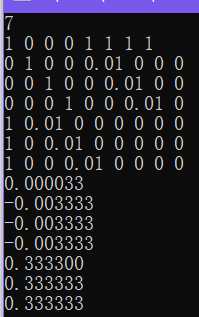
将上述增广方程组直接使用高斯消元出解，同样的，当eps>=0.01结果会出现误差，如下图所示：

(c)豪斯霍尔德QR分解

void Maqr(Complex &A)
{
    double u, alpha, w, t;
    if (A.m < A.n)
    {
        cout << "\nQR分解失败！" << endl;
        exit(1);
    }
    Complex Q;
    Q.n = A.m;
    Q.m = A.m;
    for (int i = 1; i <= A.m; i++)
        for (int j = 1; j <= A.m; j++)
        {
            Q.a[i][j] = 0.0;
            if (i == j) Q.a[i][j] = 1.0;
        }
    int nn = A.n;
    if (A.m == A.n) nn = A.m - 1;
    for (int k = 1; k <= nn; k++)
    {
        u = 0.0;
        for (int i = k; i <= A.m; i++)
        {
            w = fabs(A.a[i][k]);
            if (w > u) u = w;
        }
        alpha = 0.0;
        for (int i = k; i <= A.m; i++)
        {
            t = A.a[i][k] / u;
            alpha = alpha + t * t;
        }
        if (A.a[k][k] > 0.0) u = -u;
        alpha = u * sqrt(alpha);
        if (fabs(alpha) + 1.0 == 1.0)
        {
            cout << "\nQR分解失败！" << endl;
            exit(1);
        }
        u = sqrt(2.0*alpha*(alpha - A.a[k][k]));
        if ((u + 1.0) != 1.0)
        {
            A.a[k][k] = (A.a[k][k] - alpha) / u;
            for (int i = k + 1; i <= A.m; i++) A.a[i][k] = A.a[i][k] / u;
            for (int j = 1; j <= A.m; j++)
            {
                t = 0.0;
                for (int jj = k; jj <= A.m; jj++)
                    t = t + A.a[jj][k] * Q.a[jj][j];
                for (int i = k; i <= A.m; i++)
                    Q.a[i][j] = Q.a[i][j] - 2.0*t*A.a[i][k];
            }

            for (int j = k + 1; j <= A.n; j++)
            {
                t = 0.0;
                for (int jj = k; jj <= A.m; jj++)
                    t = t + A.a[jj][k] * A.a[jj][j];
                for (int i = k; i <= A.m; i++)
                    A.a[i][j] = A.a[i][j] - 2.0*t*A.a[i][k];
            }
            A.a[k][k] = alpha;
            for (int i = k + 1; i <= A.m; i++)  A.a[i][k] = 0.0;
        }
    }
    for (int i = 1; i <= A.m; i++)
        for (int j = i + 1; j <= A.m; j++)
        {
            t = Q.a[i][j]; Q.a[i][j] = Q.a[j][i]; Q.a[j][i] = t;
        }
    cout << "Q:" << endl;
    cout << Q;
    Complex QT = !Q;
    Complex b;
    b.m = 4;
    b.n = 1;
    b.a[1][1] = 1; b.a[2][1] = 0; b.a[3][1] = 0; b.a[4][1] = 0;
    Complex c1 = QT * b;
    cout << "Q^T b:" << endl;
    cout << c1;
    cout << "R" << endl;
    cout << A;
}

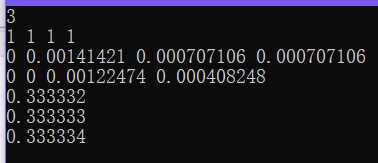
当eps = 0.01时，有QR分解结果如下：

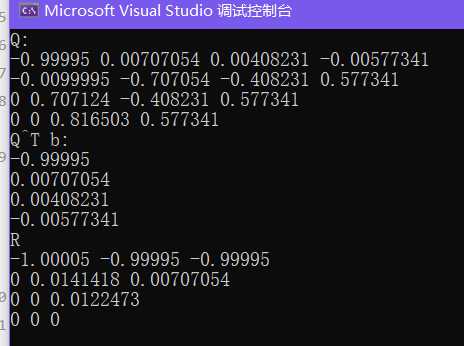
最小二乘解如下:

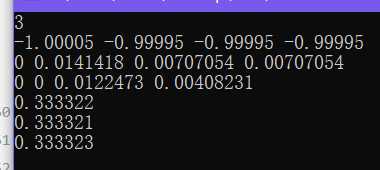
可以发现存在一定误差，当eps = 0.001时，仍然存在误差，QR分解结果如下：

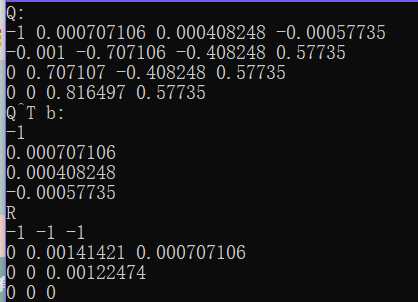
最小二乘解如下：

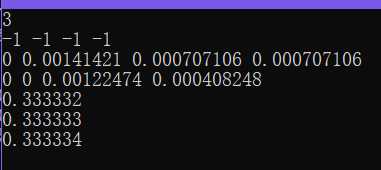
(d)吉文斯QR分解

void Givens(Complex &A, Complex &b)
{
    Complex I;
    I.m = A.m;
    I.n = A.m;
    for (int i = 1; i <= A.m; i++)
    {
        for (int j = 1; j <= A.m; j++)
            if (i == j) I.a[i][j] = 1;
                else I.a[i][j] = 0;
    }
    Complex G1 = I;
    G1.a[1][1] = A.a[1][1]/sqrt(A.a[1][1] * A.a[1][1] + A.a[2][1] * A.a[2][1]);
    G1.a[2][2] = G1.a[1][1];
    G1.a[1][2] = A.a[2][1]/sqrt(A.a[1][1] * A.a[1][1] + A.a[2][1] * A.a[2][1]);
    G1.a[2][1] = -G1.a[1][2];
    cout << "G1:" << endl;
    cout << G1;
    A = G1 * A;
    b = G1 * b;
    cout << "A:" << endl;
    cout << A;
    cout << "b:" << endl;
    cout << b;
    Complex G2 = I;
    G2.a[2][2] = A.a[2][2]/sqrt(A.a[2][2] * A.a[2][2] + A.a[3][2] * A.a[3][2]);
    G2.a[3][3] = G2.a[2][2];
    G2.a[2][3] = A.a[3][2]/sqrt(A.a[2][2] * A.a[2][2] + A.a[3][2] * A.a[3][2]);
    G2.a[3][2] = -G2.a[2][3];
    cout << "G2:" << endl;
    cout << G2;
    A = G2 * A;
    b = G2 * b;
    cout << "A:" << endl;
    cout << A;
    cout << "b:" << endl;
    cout << b;
    Complex G3 = I;
    G3.a[3][3] = A.a[3][3]/sqrt(A.a[3][3] * A.a[3][3] + A.a[4][3] * A.a[4][3]);
    G3.a[4][4] = G3.a[3][3];
    G3.a[3][4] = A.a[4][3]/sqrt(A.a[3][3] * A.a[3][3] + A.a[4][3] * A.a[4][3]);
    G3.a[4][3] = -G3.a[3][4];
    cout << "G3:" << endl;
    cout << G3;
    A = G3 * A;
    b = G3 * b;
    cout << "A:" << endl;
    cout << A;
    cout << "b:" << endl;
    cout << b;
}

吉文斯QR分解的精度与豪斯霍尔德QR分解的精度相似，在eps=0.001时有微小误差，吉文斯QR分解结果如下图：

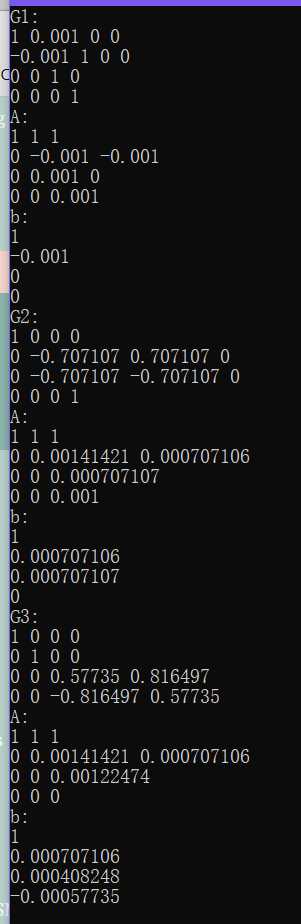
最小二乘解如下：

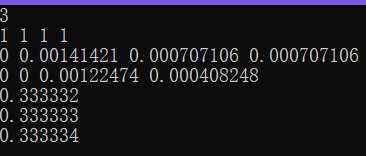
(e)古典格拉姆-施密特正交化

void GramSchmidt(Complex &A, Complex &B)
{
    Complex R, Q;
    Q.n = A.m;
    Q.m = A.m;
    for (int i = 1; i <= A.m; i++)
        for (int j = 1; j <= A.m; j++)
        {
            Q.a[i][j] = R.a[i][j] = 0;
        }
    R.m = A.m;
    R.n = A.n;
    double a[10], b[10];
    for (int j = 1; j <= A.m; j++)
    {
        for (int i = 1; i <= A.m; i++)
            a[i] = b[i] = A.a[i][j];
        for (int i = 1; i < j; i++)
        {
            R.a[i][j] = 0;
            for (int m = 1; m <= A.m; m++)
                R.a[i][j] += a[m] * Q.a[m][i];
            for (int m = 1; m <= A.m; m++)
                b[m] -= R.a[i][j] * Q.a[m][i];
        }
        double f2 = 0;
        for (int i = 1; i <= A.m; i++)
            f2 += b[i] * b[i];
        f2 = sqrt(f2);
        R.a[j][j] = f2;
        if (f2 == 0) break;
        for (int i = 1; i <= A.m; i++)
            Q.a[i][j] = b[i] / f2;
    }
    cout << "Q:" << endl;
    cout << Q;
    cout << "R:" << endl;
    cout << R;  
    Complex QT = !Q;
    Complex c1 = QT * B;
    cout << "Q^T b"<<endl;
    cout << c1;
}

当esp=0.001时，QR分解的结果如下：

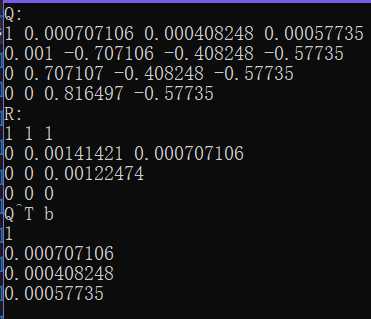
最小二乘问题解如下：

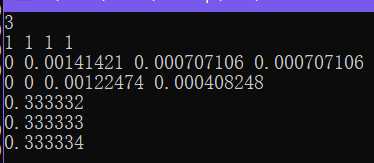
(f)改进格拉姆-施密特正交化

void GramSchmidt(Complex &A, Complex &B)
{
    Complex R, Q;
    Q.n = A.m;
    Q.m = A.m;

    R.m = A.m;
    R.n = A.n;
    for (int j = 1; j <= A.m; j++)
    {
        double f2 = 0;
        for (int i = 1; i <= A.m; i++)
            f2 += A.a[i][j] * A.a[i][j];
        f2 = sqrt(f2);
        if (f2 == 0) break;
        R.a[j][j] = f2;
        for (int i = 1; i <= A.m; i++)
            Q.a[i][j] = A.a[i][j] / f2;

        for (int i = j + 1; i <= A.m; i++)
        {
            R.a[i][j] = 0;
            for (int m = 1; m <= A.m; m++)
                R.a[j][i] += A.a[m][i] * Q.a[m][j];
            for (int m = 1; m <= A.m; m++)
                A.a[m][i] -= R.a[j][i] * Q.a[m][j];
        }


    }
    cout << "Q:" << endl;
    cout << Q;
    cout << "R:" << endl;
    cout << R;  
    Complex QT = !Q;
    Complex c1 = QT * B;
    Complex c2 = Q * R;
    //cout << c2;
    cout << "Q^T b"<<endl;
    cout << c1;
}

当esp=0.001时，QR分解结果如下：

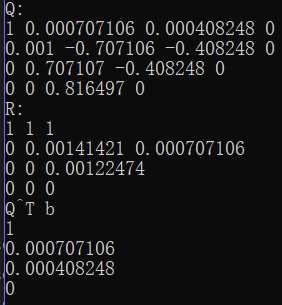
最小二乘解如下：

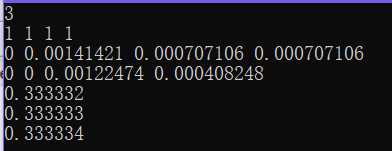
(g)带有迭代改良的古典格拉姆-施密特正交化

书上的说法是

对任何格拉姆-施密特程序来讲,通过重新正交化可进一步增强矩阵 $Q_1$ 的正交性，即重复得到 $Q_1$ 的过程.这种重新正交化可用迭代改良的形式来完成,通常一次重新正交化就可得到较为满意的结果.(两次使用CGS)

书上也并没有过多的解释，我只能推测是两次执行古典格拉姆-施密特正交化即可

void GramSchmidt(Complex &A, Complex &B)
{
    Complex R, Q;
    Q.n = A.m;
    Q.m = A.m;
    R.m = A.m;
    R.n = A.n;
    double b[10], a[10];
    for (int l = 1; l <= 2; l++)
    {
        for (int j = 1; j <= A.m; j++)
        {
            for (int i = 1; i <= A.m; i++)
                a[i] = b[i] = A.a[i][j];
            for (int i = 1; i < j; i++)
            {
                R.a[i][j] = 0;
                for (int m = 1; m <= A.m; m++)
                    R.a[i][j] += a[m] * Q.a[m][i];
                for (int m = 1; m <= A.m; m++)
                    b[m] -= R.a[i][j] * Q.a[m][i];
            }
            double f2 = 0;
            for (int i = 1; i <= A.m; i++)
                f2 += b[i] * b[i];
            f2 = sqrt(f2);
            R.a[j][j] = f2;
            if (f2 == 0) break;
            for (int i = 1; i <= A.m; i++)
                Q.a[i][j] = b[i] / f2;
        }


    }
    cout << "Q:" << endl;
    cout << Q;
    cout << "R:" << endl;
    cout << R;  
    Complex QT = !Q;
    Complex c1 = QT * B;
    Complex c2 = Q * R;
    cout << c2;
    cout << "Q^T b"<<endl;
    cout << c1;
}

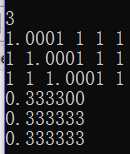
和普通的古典格拉姆-施密特正交化一样在esp=0.001时有微小误差：

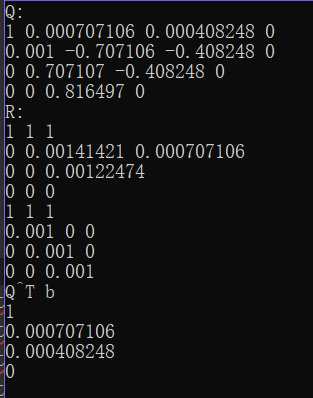
(h)奇异值分解

设A是m* n的矩阵，且rank(A)=n，则A的奇异值分解为

$A=U \Sigma V^T = \begin{pmatrix} U_1&U_2\\ \end{pmatrix} \begin{pmatrix} \Sigma_1\\ 0\\ \end{pmatrix} V^T =U_1\Sigma_1 V^T$

其中 $U_1$ 是m* n矩阵 $\Sigma_1$ 是n * n非奇异矩阵，最小二乘问题 $Ax\cong b$ 的解可由

$x = V\Sigma_1^{-1}U_1^Tb$

给出。
书本里面也没有给出奇异值分解的具体解法，在这里使用Mathematica对上述矩阵进行奇异值分解：

A = {{1, 1, 1}, {0.01, 0, 0}, {0, 0.01, 0}, {0, 0, 0.01}};
{u, w, v} = SingularValueDecomposition[A];
u1 = u[[{1, 2, 3, 4}, {1, 2, 3}]] ;

w1 = w[[{1, 2, 3}]];
w1i = Inverse[w1];
b = {1, 0, 0, 0};
x = v . w1i . Transpose[u1] . b;
x // MatrixForm

得到的答案为

$\begin{pmatrix} 0.333322\\ 0.333322\\ 0.333322\\ \end{pmatrix}$

若eps取0.001则可以得到精确解0.333333