牛顿法
对于可微函数进行泰勒展开,可得
$$f(x+s)\approx f(x) + J_f(x)s$$
其中,$J_f(x)$是$f$的雅可比矩阵,那么对于给出的上式,由非线性方程组的牛顿法:
$$J_f(x_k)s_k=-f(x_k)$$
$$x_{k+1}=x_k+s_k$$
代码如下:
#include <stdio.h>
#include <cmath>
#include <cstdlib>
#include <iostream>
using namespace std;
#define N 100
const float eps = 0.0000001;
double b[N], x[N];
float r[N];
float a[N][N];
double A[N][N];
float ans[N];
int n;
int select(int x) //部分选主元
{
int f = x;
for (int i = x + 1; i <= n; i++)
if (fabs(a[i][x]) > fabs(a[f][x]))
f = i;
if (f != x)
{
for (int i = x; i <= n + 1; i++)
swap(a[f][i], a[x][i]);
}
return 0;
}
int Gauss()
{
float t;
for (int i = 1; i <= n; i++)
{
select(i);
if (fabs(a[i][i]) <= eps)
{
printf("No Answers\n");
return 0;
}
for (int j = i + 1; j <= n; j++)
{
if (fabs(a[j][i]) > eps)
{
t = a[i][i] / a[j][i];
for (int k = i; k <= n + 1; k++)
a[j][k] = a[j][k] * t - a[i][k];
}
}
}
//解出答案
for (int i = n; i; i--)
{
for (int j = i + 1; j <= n; j++)
{
a[i][n + 1] -= a[i][j] * a[j][n + 1];
}
a[i][n + 1] /= a[i][i];
}
return 0;
}
int main()
{
n = 2; //未知数个数
double x0 = 4, y0 = 0.5; //初值
for (int i = 1; i <= 100; i++) // 迭代次数
{
a[1][1] = -1 + 4 * y0; a[1][2] = 4 * x0; a[2][1] = -y0; a[2][2] = -x0 - 2 * y0; //定义雅可比矩阵
a[1][3] = -(5 * x0 * y0 - x0 * (1 + y0)); a[2][3] = -(-x0 * y0 + (1 - y0) * (1 + y0));
Gauss();
x0 += a[1][3];
y0 += a[2][3];
}
printf("x = %.4lf \n y = %.4lf", x0, y0);
return 0;
}





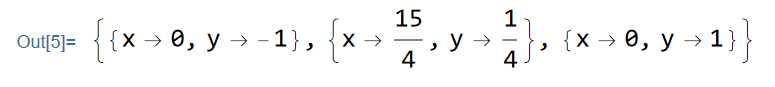
Comments NOTHING