这里是中山大学智能车队航天物流组负责人,今年是第二年参加线上赛,本人从去年开始即负责任务四最短路算法的相关内容,两年都在这个任务上拿到了满分,由于也不知道明年是否继续参赛,同时也是本着分享的精神,在这里简单介绍一下我们采用的方案与报告攥写上的一些心得。
引言
作为一个退役OIer,在看待最短路问题的时候,我是从最底层的算法原理出发,先编写基于该算法的最简易代码,然后再深入向上探讨算法的引申问题。为了将要求的最短路径算法相关内容完整的展现出来,我们使用的流程是:理论分析——基本原理代码编写——结合SLAM建图进行最短路生成——rviz建图测试——gazebo仿真最短路测试——实车最短路测试。经过以上的步骤来最终得到一个较为全面且完整的算法介绍。在这里就关键介绍今年的A*算法有关内容,去年包含的Dij算法就暂时略去。
A*的基本实现
关于A* 算法的有关原理有很多资料可以参考,就不再讲了,算法的实现上面使用的是C++,以下代码是根据有关原理写出来的,采用的是邻接矩阵加STL优先队列的方法进行实现。
在算法竞赛中,使用邻接矩阵一般来说都不是最优解,使用的更多的是称为邻接表的存储方式,但是对于实际问题来说,邻接表往往会直接退化为邻接矩阵,所以就不必再采用较为复杂的存储方式了。
算法的核心部分在于使用优先队列来维护A*中的openlist,即
priority_queue<Astar, vector<Astar>, cmp > openlist;
比较函数为
struct cmp
{
int operator()(Astar a, Astar b)
{
if (a.F != b.F)
return a.F > b.F;
else return a.G < b.G;
}
};
A*的主体实现如下
void A_star()
{
priority_queue<Astar, vector<Astar>, cmp > openlist;
Astar st = {stx, sty, 0, 0};
G[stx][sty] = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
G[i][j] = 0x7fffffff;
openlist.push(st);
closelist[stx][sty] = 1;
while (!openlist.empty())
{
Astar now = openlist.top();
closelist[now.x][now.y] = 1;
openlist.pop();
for (int i = -1; i <= 1; i++)
for (int j = -1; j <= 1; j++)
if ((i != 0 || j != 0) && (now.x + i) <= n && (now.x + i) >= 1 && (now.y + j) <= m && (now.y + j) >= 1)
{
if ((i == 0 || j == 0) && closelist[now.x + i][now.y + j] != 1 && G[now.x + i][now.y + j] > now.G + 10 && map[now.x + i][now.y + j] > 10 && check(now.x, now.y))
{
Astar next = { now.x + i, now.y + j, now.G + 10,now.G + 10 + get(now.x + i, now.y + j) };
fa[now.x + i][now.y + j] = { now.x, now.y };
G[now.x + i][now.y + j] = now.G + 10;
F[now.x + i][now.y + j] = next.F;
if (now.x + i == edx && now.y + j == edy) return;
openlist.push(next);
}
else if (i != 0 && j != 0 && closelist[now.x + i][now.y + j] != 1 && G[now.x + i][now.y + j] > now.G + 14 && map[now.x + i][now.y + j] > 10 && map[now.x + i][now.y] > 10 && map[now.x][now.y + j] > 10 && check(now.x, now.y))
{
Astar next = { now.x + i, now.y + j, now.G + 14,now.G + 14 + get(now.x + i, now.y + j) };
fa[now.x + i][now.y + j] = { now.x, now.y };
G[now.x + i][now.y + j] = now.G + 14;
F[now.x + i][now.y + j] = next.F;
if (now.x + i == edx && now.y + j == edy) return;
openlist.push(next);
}
}
}
}
本质上就是将地图的对角线长度计为14,临边长度计为10,然后进行A*算法,此处使用整数的原因则是若将这个数存储为浮点型,可能会带来没必要的额外运算开支。
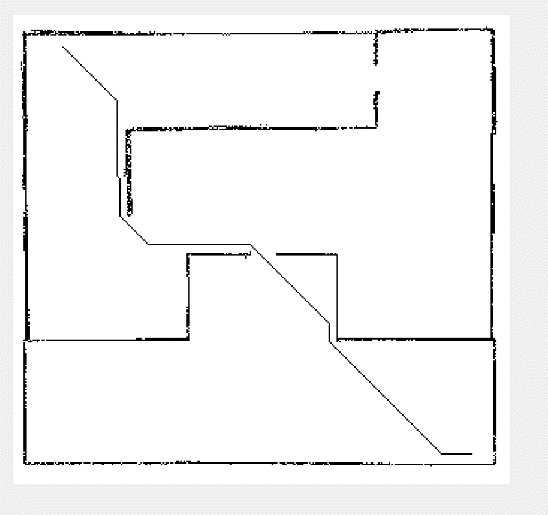
在A*代码完成后,将其与SLAM建图结果结合即可实现如下效果:
实现的办法是将SLAM建图结果保存为图片,在Matlab中即可提取得到图片的灰度信息,将转化为灰度后的数字作为地图放入算法中就可以实现类似的效果。需要注意的是,在上述A*实现中,为了保证路径不是贴着墙壁的(理论上贴墙路径最优),需要进行一些特判以实现最终路径距离边界能够留出一段距离的效果。
在Rviz中的算法测试
这一部分,即三院要求的部分,要想实现明显的效果对比其实只需要两点:找到固定地图的方法、找到提供的代码中的坑。
首先是固定地图的方案,线上赛教学中并没有给出,而是使用了同时显示两条路径的方法,但是那种方案过于复杂,需要对ROS有一定的了解才能实现。
在文件random_complex_generator.cpp中,我们可以很快的找到有关随机地图生成的函数:
void RandomMapGenerate()
{
random_device rd;
default_random_engine eng(rd());
此处的random_device是一个随机数种子生成器,而default_random_engine则是根据rd生成的随机数种子进行随机数生成。
在这里说一下随机数种子的概念,若想要生成一串随机数序列,一般需要一个随机数种子,使用同一个种子生成的随机序列是一样的。举个例子,随机数种子是100,无论生成多少次,得到的随机数序列永远是[8 4 3 2 5 8 6 4 7 ...],即该序列内部的各个数值之间的关系是随机的,但是该序列是唯一的。一般来说,在算法竞赛里面,我们会使用系统时间作为随机数种子,但是如果两次执行程序的时间过于接近,那么得到的结果也会是一样的。
回到这个随机地图生成函数上来,跟上面说的一样,只要固定了随机数种子那么得到的随机数序列就会是一样的,那么我们将随机数种子生成器rd()换成一个固定值,那么就可以固定地图:
void RandomMapGenerate()
{
default_random_engine eng(100);
将随机数种子设置为100,此时再次重新执行roslaunch,可以发现地图已经不再发生变化,这样就可以进行接下来的操作。
首先是默认A*算法的测试,三种启发函数的效果基本一致,这里取其中一种,如下:

其性能如下

这里需要注意的一点是,组委会提供的代码是有坑的,具体坑在哪里读过代码的应该都能发现,需要将那个小bug修复一下才能看出效果。
优化上我们使用的是最最简单的$ε-admissible$方案,直接在启发函数上乘一个大于1的系数,加大A* 算法在扩展每一个节点时的代价,最终导致的结果就是静态加权后的A*算法扩展的结点比原来更少,从而加快运行速度。
可以发现在优化后有明显的区别:


可以看到,此时得到路径的最优性并没有减弱太多,但是相比于最初的启发函数来说,其路径依然是由明显的变化的,但是牺牲最优性,换来的是运行时间得到有效缩短,在进行了启发函数优化后,运行的时间从0.1ms降低到了0.04ms,搜索的节点数量从44降低到了26,大大加快了算法的运行速度,同时由于A*需要维护一个节点队列,该改进方案也节约了很大的内存空间。
除了最简单的$ε-admissible$算法之外,还有很多其他的有关算法,在这里我们就没有更多的进行测试了。
gazebo 仿真与实车最短路测试
这一个方面并没有什么好说的地方了,在报告中主要体现的是在仿真与实际运行中的寻路是基于全局最短路与局部最短路两种算法结合来完成的;同时其地图也是有一定膨胀的局部代价地图与全局代价地图来防止碰撞的发生,这与前面A*在SLAM建图上运行的思路是有一定相似之处的。
任务四的大概内容就介绍到这里,说实话能得满分还是意料之外的,本质上只是将要求的体现改进算法的区别,在此基础上额外做了一些其他工作而已。





Comments NOTHING