转载,复制,请遵循文末链接CC BY-NC-SA 4.0国际许可协议
带位移的反幂法
#include <stdio.h>
#include <cmath>
#include <cstdlib>
#include <iostream>
using namespace std;
#define N 100
#define MAXN 20
const float eps = 0.0000001;
float b[N],x[N];
float r[N];
float a[N][N];
float A[N][N];
float ans[N];
int n;
int select(int x) //部分选主元
{
int f = x;
for (int i = x + 1; i <= n; i++)
if (fabs(a[i][x]) > fabs(a[f][x]))
f = i;
if (f != x)
{
for (int i = x; i <= n + 1; i++)
swap(a[f][i], a[x][i]);
}
return 0;
}
int Gauss()
{
float t;
for (int i = 1; i <= n; i++)
{
select(i);
if (fabs(a[i][i]) <= eps)
{
printf("No Answers\n");
return 0;
}
for (int j = i + 1; j <= n; j++)
{
if (fabs(a[j][i]) > eps)
{
t = a[i][i] / a[j][i];
for (int k = i; k <= n + 1; k++)
a[j][k] = a[j][k] * t - a[i][k];
}
}
}
//解出答案
for (int i = n; i; i--)
{
for (int j = i + 1; j <= n; j++)
{
a[i][n + 1] -= a[i][j] * a[j][n + 1];
}
a[i][n + 1] /= a[i][i];
}
return 0;
}
int main()
{
double s = 0; //位移
n = 3;
A[1][1] = a[1][1] = 6 - s;
A[1][2] = a[1][2] = 2;
A[1][3] = a[1][3] = 1;
A[2][1] = a[2][1] = 2;
A[2][2] = a[2][2] = 3 - s;
A[2][3] = a[2][3] = 1;
A[3][1] = a[3][1] = 1;
A[3][2] = a[3][2] = 1;
A[3][3] = a[3][3] = 1 - s;
a[1][4] = 1; a[2][4] = 2; a[3][4] = 2;//初始向量
for (int i = 1; i <= MAXN; i++)
{
Gauss();
float sum = 0;
for (int j = 1; j <= n; j++)
sum += a[j][n + 1] * a[j][n + 1];
float r = sqrt(sum);
printf("%d : %f\n", i, 1 / r + s);
for (int j = 1; j <= n; j++)
a[j][n + 1] /= r;
double p = 1 / a[n][n + 1];
printf("%f %f 1\n", a[1][n + 1] * p, a[2][n + 1] * p);
for (int j = 1; j <= n; j++)
for (int k = 1; k <= n; k++)
a[j][k] = A[j][k];
}
return 0;
}
验证如下:
使用mathematica直接计算矩阵的特征值:
可以得到特征值如下:

与反幂法所得结果一致。
另外,测试位移为7时,输出结果如下:
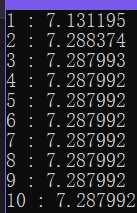
可以看出,反幂法的收敛速度很快,而且可以得到很精确的解
相比于特征值,想要得到让特征向量收敛到一个较为精确的解,所需要的迭代次数更多,如下图所示:
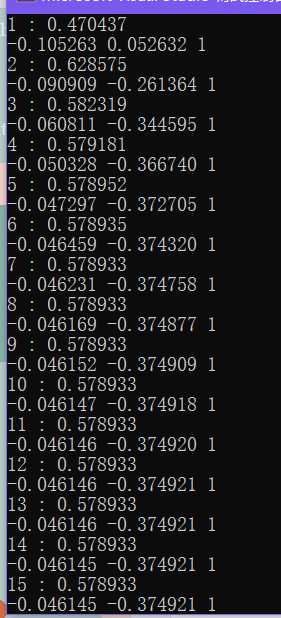
将得到的特征向量和mathematica中得到的解对比,发现几乎没有误差,如下:

带位移的QR迭代法
#include <iostream>
#include <stdio.h>
#include <cmath>
using namespace std;
#define eps 0.001
#define MAXN 10
class Complex
{
public:
Complex()
{
for (int i = 0; i <= 9; i++)
for (int j = 0; j <= 9; j++)
a[i][j] = 0;
n = 0; m = 0;
}
friend Complex operator +(Complex& c1, Complex& c2);
friend Complex operator -(Complex& c1, Complex& c2);
friend Complex operator *(Complex& c1, Complex& c2);
friend Complex operator !(Complex& c1);
friend ostream& operator <<(ostream&, Complex&);
friend istream& operator >>(istream&, Complex&);
double a[10][10]; //定义矩阵,矩阵中a[i][j]表示复数的实部,a[i][j][1]表示复数的虚部
int n, m; //标识矩阵的大小,由用户输入
};
Complex A, Q;
Complex operator +(Complex& c1, Complex& c2) //矩阵加法的重载实现
{
Complex c3;
if (c1.m != c2.m || c1.n != c2.n) //判断是否能够进行矩阵加法
{
printf("这两个矩阵不能相加\n");
return c3;
}
c3.m = c1.m;
c3.n = c1.n;
for (int i = 1; i <= c1.m; i++)
for (int j = 1; j <= c1.n; j++)
{
c3.a[i][j] = c1.a[i][j] + c2.a[i][j];
// c3.a[i][j][1] = c1.a[i][j][1] + c2.a[i][j][1];
}
return c3;
}
Complex operator -(Complex& c1, Complex& c2) //矩阵减法的重载实现
{
Complex c3;
if (c1.m != c2.m || c1.n != c2.n) //判断是否能够进行矩阵减法
{
printf("这两个矩阵不能相减\n");
return c3;
}
c3.m = c1.m;
c3.n = c1.n;
for (int i = 1; i <= c1.m; i++)
for (int j = 1; j <= c1.n; j++)
{
c3.a[i][j] = c1.a[i][j] - c2.a[i][j];
// c3.a[i][j][1] = c1.a[i][j][1] - c2.a[i][j][1];
}
return c3;
}
Complex operator *(Complex& c1, Complex& c2) //矩阵乘法的实现
{
Complex c3;
if (c1.n != c2.m) //判断能否进行矩阵乘法
{
printf("这两个矩阵不能相乘\n");
return c3;
}
c3.m = c1.m;
c3.n = c2.n;
double s1 = 0, s2 = 0;
for (int i = 1; i <= c1.m; i++)
{
for (int m = 1; m <= c2.n; m++)
{
for (int j = 1; j <= c1.n; j++)
{
s1 += c1.a[i][j] * c2.a[j][m];
// s2 += c1.a[i][j] * c2.a[j][m][1] + c1.a[i][j][1] * c2.a[j][m];
}
c3.a[i][m] = s1;
// c3.a[i][m][1] = s2;
s1 = 0;
// s2 = 0;
}
}
return c3;
}
Complex operator !(Complex& c1) //矩阵转置的实现
{
Complex c2;
c2.n = c1.m;
c2.m = c1.n;
for (int i = 1; i <= c1.m; i++)
for (int j = 1; j <= c1.n; j++)
{
c2.a[j][i] = c1.a[i][j];
// c2.a[j][i][1] = -c1.a[i][j][1];
}
return c2;
}
ostream & operator << (ostream & output, Complex &c) //矩阵输出
{
for (int i = 1; i <= c.m; i++)
{
for (int j = 1; j <= c.n; j++)
output << c.a[i][j] << ' ';
output << endl;
}
return output;
}
istream & operator >> (istream & input, Complex &c) //矩阵输入
{
printf("请输入矩阵的大小:\n");
input >> c.m >> c.n; //先输入该矩阵的大小
printf("请输入矩阵:\n");
for (int i = 1; i <= c.m; i++)
{
for (int j = 1; j <= c.n; j++)
input >> c.a[i][j];
}
return input;
}
void Maqr()
{
double u, alpha, w, t;
if (A.m < A.n)
{
cout << "\nQR分解失败!" << endl;
exit(1);
}
Q.n = A.m;
Q.m = A.m;
for (int i = 1; i <= A.m; i++)
for (int j = 1; j <= A.m; j++)
{
Q.a[i][j] = 0.0;
if (i == j) Q.a[i][j] = 1.0;
}
int nn = A.n;
if (A.m == A.n) nn = A.m - 1;
for (int k = 1; k <= nn; k++)
{
u = 0.0;
for (int i = k; i <= A.m; i++)
{
w = fabs(A.a[i][k]);
if (w > u) u = w;
}
alpha = 0.0;
for (int i = k; i <= A.m; i++)
{
t = A.a[i][k] / u;
alpha = alpha + t * t;
}
if (A.a[k][k] > 0.0) u = -u;
alpha = u * sqrt(alpha);
if (fabs(alpha) + 1.0 == 1.0)
{
cout << "\nQR分解失败!" << endl;
exit(1);
}
u = sqrt(2.0 * alpha * (alpha - A.a[k][k]));
if ((u + 1.0) != 1.0)
{
A.a[k][k] = (A.a[k][k] - alpha) / u;
for (int i = k + 1; i <= A.m; i++) A.a[i][k] = A.a[i][k] / u;
for (int j = 1; j <= A.m; j++)
{
t = 0.0;
for (int jj = k; jj <= A.m; jj++)
t = t + A.a[jj][k] * Q.a[jj][j];
for (int i = k; i <= A.m; i++)
Q.a[i][j] = Q.a[i][j] - 2.0 * t * A.a[i][k];
}
for (int j = k + 1; j <= A.n; j++)
{
t = 0.0;
for (int jj = k; jj <= A.m; jj++)
t = t + A.a[jj][k] * A.a[jj][j];
for (int i = k; i <= A.m; i++)
A.a[i][j] = A.a[i][j] - 2.0 * t * A.a[i][k];
}
A.a[k][k] = alpha;
for (int i = k + 1; i <= A.m; i++) A.a[i][k] = 0.0;
}
}
for (int i = 1; i <= A.m; i++)
for (int j = i + 1; j <= A.m; j++)
{
t = Q.a[i][j]; Q.a[i][j] = Q.a[j][i]; Q.a[j][i] = t;
}
// cout << "Q:" << endl;
//cout << Q;
// cout << "R" << endl;
// cout << A;
}
int main()
{
A.m = 3;
A.n = 3;
A.a[1][1] = 6; A.a[1][2] = 2; A.a[1][3] = 1;
A.a[2][1] = 2; A.a[2][2] = 3; A.a[2][3] = 1;
A.a[3][1] = 1; A.a[3][2] = 1; A.a[3][3] = 1;
double s = A.a[3][3]; //位移
Complex I;
I.m = 3;
I.n = 3;
I.a[1][1] = s; I.a[1][2] = 0; I.a[1][3] = 0;
I.a[2][1] = 0; I.a[2][2] = s; I.a[2][3] = 0;
I.a[3][1] = 0; I.a[3][2] = 0; I.a[3][3] = s;
for (int i = 1; i <= MAXN; i++)
{
cout << i << ":" << endl;
I.a[1][1] = I.a[2][2] = I.a[3][3] = A.a[3][3];
A = A - I;
Maqr();
A = A * Q;
A = A + I;
cout << A;
}
}
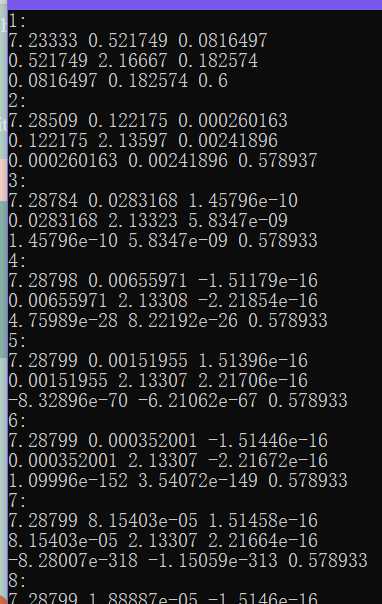
可以发现,在第五次迭代时,带位移的QR分解就已经得到了较为精确的特征值。






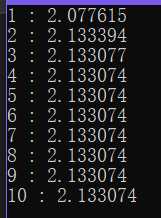
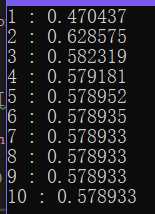
Comments NOTHING