实验原理

基于FIR噪声整形技术

在本次仿真实验中，噪声整形技术是为了减少数字信号在进行DAC后引入的量化误差，如图1.1(b)所示，在进行量化后，在信号频带内出现了量化导致的频率分量，而这个频率分量是较为宽的。我们可以设计一个FIR滤波器，使得其结构入图1.1(a)所示，这也可以降低量化噪声在有效信号频带内的大小，而增大其在信号带外的分量。

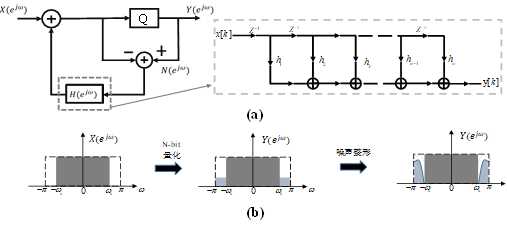
其中，若以$N(e^{j\omega})$表示量化引入的噪声，$X(e^{j\omega})$为未量化的信号，那么输出$Y(e^{j\omega})$可以表示为：

$$Y(e^{j\omega})=X(e^{j\omega})+(1+H(e^{j\omega}))N(e^{j\omega})$$

我们观察量化噪声的频谱，如图1.2所示，可以发现其在全频带上均匀分布，也就是说其对信号带内和带外均有影响。通过FIR滤波器$H(e^{j\omega})$可以抑制带内噪声，从而提高信号的可靠性。

为了抑制通带内的量化噪声，噪声在经过了FIR滤波器后的功率应小于原本的功率，即：

$$\int \vert 1+H(e^{j\omega })\vert^2 N(e^{j\omega }) d\omega < \int N(e^{j\omega }) d\omega$$

假设FIR滤波器可以表示为：

$$H(z)=h_1 z^{-1} + h_2 z^{-2} + \cdots + h_M z^{-M}$$

上述问题可以转化为优化问题:

$$\min_{h_1, h_2,\ldots,h_M} \int \vert 1+H(e^{j\omega })\vert^2 d\omega$$

若设

$$
A= \begin{bmatrix}
e^{-j\omega_1} & e^{-j2\omega_1} & \ldots & e^{-jM\omega_1} \cr e^{-j\omega_2} & e^{-j2\omega_2} & \ldots & e^{-jM\omega_2} \cr \vdots & \vdots & \ddots & \vdots \cr e^{-j\omega_P} & e^{-j2\omega_P} & \ldots & e^{-jM\omega_P} \end{bmatrix}$$

上述优化问题的解就是：

$${\bf h_{{\rm opt}}} = -\begin{bmatrix}A_r \cr A_i\end{bmatrix}^\dagger \begin{bmatrix}\bf 1 \cr \bf 0\end{bmatrix}$$

上述方案只对信号带内进行约束，可能会导致信号带内的噪声仍然较大。如果引入一个加权矩阵$W = diag(W_1,W_2,\ldots,W_P, W_{P+1},W_{P+2}, \ldots, W_{P+Q})$，上述优化问题变为：

$$\min_{{\bf h}} \Vert W({\bf 1}+A{\bf h})\Vert_2^2$$

假设带内分量为$W_1,W_2,\ldots,W_P$，表示为$W_S$；带外分量为$W_{P+1},\ldots,W_{P+Q}$，表示为$W_I$。为了抑制带内噪声，需要有$W_S \gg W_I$。此时，有：

$$A= \begin{bmatrix} e^{-j\omega_1} & e^{-j2\omega_1} & \ldots & e^{-jM\omega_1} \cr e^{-j\omega_2} & e^{-j2\omega_2} & \ldots & e^{-jM\omega_2} \cr \vdots & \vdots & \ddots & \vdots \cr e^{-j\omega_{P+Q}} & e^{-j2\omega_{P+Q}} & \ldots & e^{-jM\omega_{P+Q}}\end{bmatrix}$$

上述优化问题最终可以写作:

$${\bf h_{{\rm opt}}} = -\begin{bmatrix}WA_r \cr WA_i\end{bmatrix}^\dagger \begin{bmatrix}\bf W1 \cr \bf 0\end{bmatrix}$$

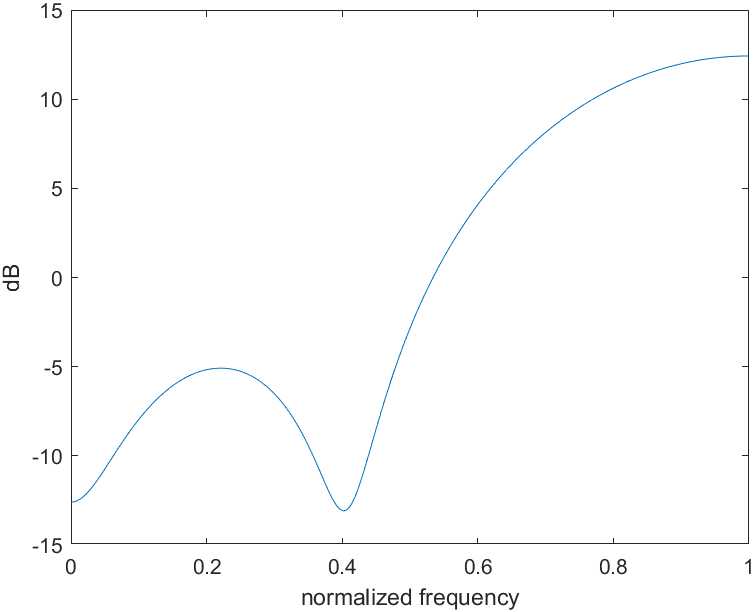
根据上述方法，取$W_S=24$，$W_I=1$，设计一个七阶FIR滤波器，其单边通带和阻带宽度均为$\frac{\pi}{2}$，通过上述方法得到的滤波器幅频响应如图1.3所示：

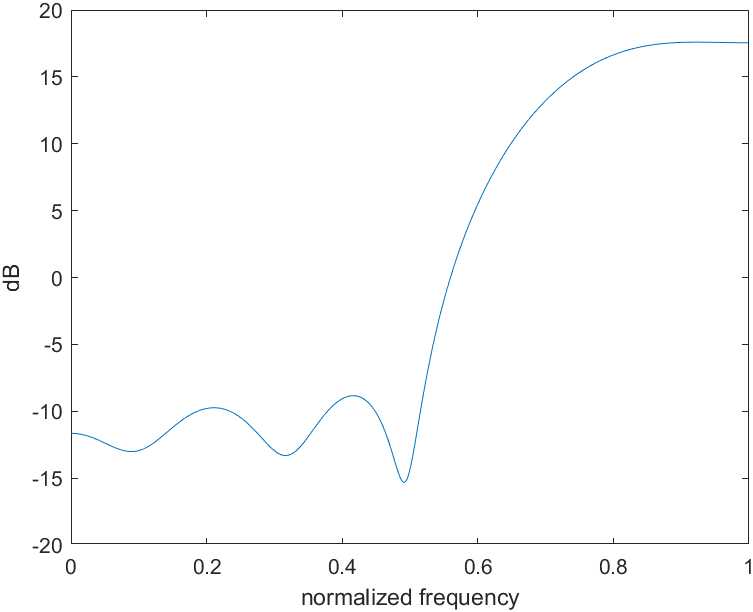
若将其与量化噪声相乘，可以得到滤波后的量化噪声频谱如图1.4所示，可以看到，在经过了噪声整形FIR滤波器后，通带内的噪声分量有效减少了，而通带外的噪声分量则增多了，这也符合噪声整形FIR滤波器的幅频响应特点。

DMT原理

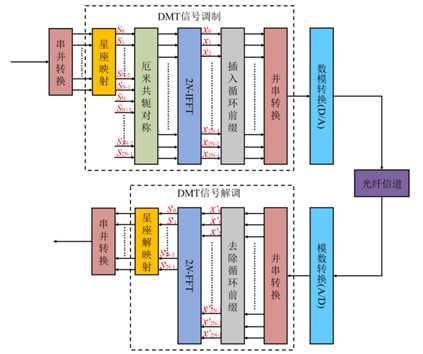
DMT信号是一种实数多载波调制信号，分别采用快速傅里叶逆变换（IFFT）和快速傅里叶变换（FFT）进行调制和解调。

首先，高速伪随机二进制序列（PRBS）通过串并转换后分解成多个并行低速信号，同时根据系统的频率响应调节每个子载波上的比特数。然后，对各个子载波进行星座映射，常用的星座映射有PAM、QAM、PSK 等。为了得到实数信号，星座映射之后进行厄米共轭对称运算，如式：

$$S_{2N-n}=S^*_n,S_0=S_N=0$$

将厄米共轭对称运算之后的数据，直接进行2N点的IFFT。 IFFT 之后得到了子载波相互正交的实数 DMT 信号。为了缓解传输过程中信道 CD 带来的 符号之间的串扰(ISI)和子载波间的干扰（ICI），同时保证子载波之间的相互正交，可以在 IFFT 之后加入循环前缀（CP）。加入 CP 会增加系统的开销，以牺牲系统带宽为代价提升性能，因此，在实际的应用中需要权衡比较传输容量和传输性能。并串转换之后就得到了基带 DMT 信号，最后在通过数模转换将数字信号转换成模拟信号后进行传输。接收端的操作是发送端的逆过程，经过信道传输后，首先将接收到的信号进行模数转换将模拟信号转化为数字信号，然后进行串并转换将串联的数据流转换为并联的数据块，接着再去除CP，进行2N点的FFT操作得到频域信号，然后进行星座解映射，最后并串转换后进行误码率（BER）的计算。流程图如图1.5所示：

VPI、MATLAB联合仿真

通过MATLAB生成随机序列，进行DMT调制后，使用FIR滤波器进行量化噪声整形，得到最终在信道中传输的序列。

而光纤信道使用的是VPI软件进行仿真测试，VPI使用Co-Simulation将MATLAB计算出来的输出序列传输到光纤中，再将经过光纤传输后的信号保存成MATLAB文件以供后续计算误码率。VPI中的仿真结构如图1.6所示：

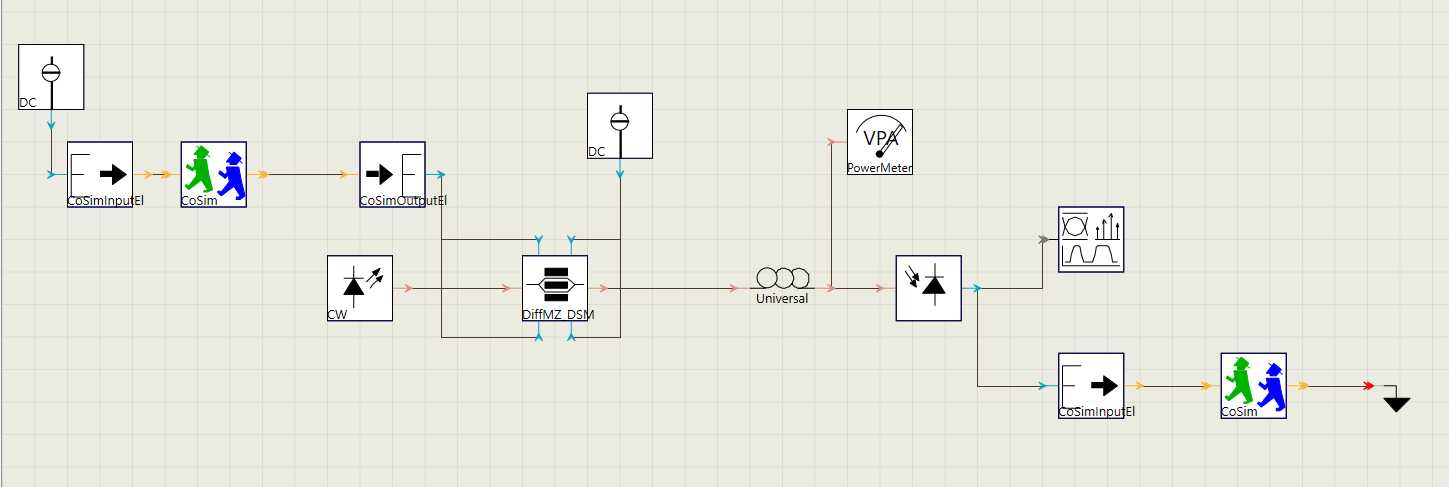
在VPI中，DSM调制器的输入光信号平均功率为$10^{-3}W$，输入数据来自MATLAB的输出文件。直流偏置使用$-1.25V$，经过光纤传输后，使用灵敏度为$1A/W$的光电二极管进行接收。并且经过传输后的信号使用光功率计进行功率测量，再将输出存储成MATLAB格式。

仿真测试时，首先在MATLAB中设置断点至存储数据后，读取数据前。运行MATLAB程序生成当此仿真的随机数据，并且进行DMT调制与FIR滤波器噪声整形。将此结果保存至.txt文件，随后运行VPI软件，等待运行结束后，继续运行MATLAB程序，进行DMT解调与误码率的计算。

在仿真测试中，使用改变光纤长度的方式调整接收光功率(ROP)，其他参数均不做改变以保证仿真结果的可靠性。

算法实现

FIR滤波器的噪声整形

首先需要进行数字量化，根据要求，我们使用4/5-bit的DAC，即占五个二进制位，小数位占四位。send为DMT调制后的信号，将其重复三次以模拟DAC的采样频率。量化后与原始数据相减得到量化噪声，随后根据1.1中的算法，得到FIR滤波器的系数h4，再使用MATLAB的函数freqz，得到滤波器的幅频响应。

    send = mapminmax(send);
    send = repelem(send, 3);
    q_type = [5,4];
    q = quantizer('fixed','round','saturate',q_type); 
    data_q = quantize(q,send); % 5bit数字量化
    noise = data_q - send; %得到量化噪声
    No = fft(noise); %得到量化噪声的频谱
    w = 0:1:20;
    D0 = exp(-1i*1/21*pi * w);
    for n = 1:7 %滤波器阶数为7
        E(:,n) = D0.^n;
    end
    w(1:12) = 24; %计算FIR滤波器系数
    w(13:21) = 1;
    W = diag(w);
    h1 = W * real(E);
    h2 = W * imag(E);
    h3 = -pinv([h1; h2])*[w.';zeros(21,1)];
    h4 = h3(:,1); %最终的FIR滤波器系数
    [h,w] = freqz([1 h4.'],1,length(No));

DMT调制解调

调制部分首先定义数据长度和调制阶数等信息，此处需要注意为了保证最后传输的数据长度满足VPI仿真的长度，需要对数据长度进行相应调整。
DMT调制解调相关原理如1.2，最终调制后得到的输出序列为send。调制部分代码如下：

N = 16;                                  % 循环前缀长度
M = 16;                                 % 调制阶数
L_data = 262144 * 2 - 32;                            % 数据长度
L_symbol = L_data/log2(M);              % 符号长度
data = round(rand(1,L_data));           % 原始数据
EbN0_dB = 12;                         % Eb/N0 dB形式
EbN0 = 10.^(EbN0_dB/10);                % 每比特能量/噪声
EsN0 = log2(M) * EbN0;                  % 每符号能量/噪声
error = zeros(1,length(EbN0_dB));       % 预置错误符号个数
detect = zeros(1,L_symbol);         % 预置检测信号
ser = zeros(1,length(EbN0_dB));         % 预置仿真误符号率
send_set = [-3+3j,-1+3j,1+3j,3+3j,...
            -3+1j,-1+1j,1+1j,3+1j,...
            -3-1j,-1-1j,1-1j,3-1j,...
            -3-3j,-1-3j,1-3j,3-3j];     % 发射端星座点


in = input216QAM(data, L_symbol);
in = in.';
S = mirror(in);                       % 厄米共轭对称
F = ifft(S);                            % IFFT
C = cp(F, N);                           % 插入循环前缀
send = C.';
\end{lstlisting}
\par
解调部分代码如下：
\begin{lstlisting}
    load('D:\VPI_Rx.mat');
    receive = Rx.band.E;
    D = decyclicpad(receive.',N);  % 去除循环前缀
    K = fft(D);                 %FFT

    T = K(1:L_symbol,:);          %取前半序列
    TT = sort(real(T));
    T = T / (TT(end - 3)/3);
    [detect, error] = de16QAM(T, in, L_symbol, M);
    20*log10(error / L_data)

解调时，为了保证信号的幅度能够归一化成16QAM的相应形式，对最终的数据进行了除最大值的处理，以便于解调。各个函数的细节部分不在此展开。

仿真测试

接收光功率测试

为了确定调整接受光功率的方案，首先测试的是是否可以通过改变光纤长度来改变接收光功率，仿真后结果如图3.1所示：

可以看见接收光功率与光纤长度成线性相关，且拟合得到的直线为$2.12851 - 0.0004 x$，即光纤长度每增加一米，接收光功率下降$0.0004dBmW$。所以我们可以使用改变光纤长度的方式，线性地改变接收光功率，下面进行的测试即使用更改光纤长度的方式调整接收光功率。

误码率与接收光功率

通过VPI仿真，分别测试直接使用量化不采用FIR滤波器的误码率与使用了噪声整形技术得到的误码率，结果如图3.2所示：

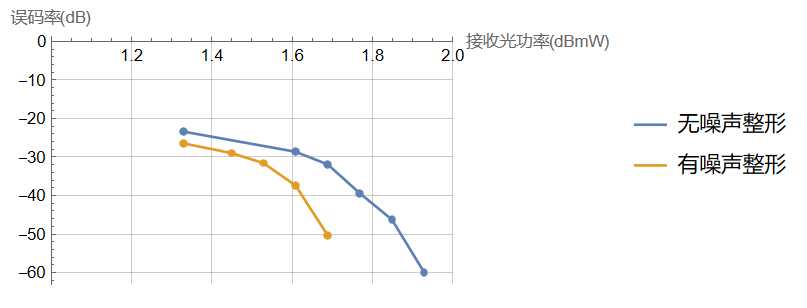
可以看到，当使用了FIR滤波器进行噪声整形后，误码率显著下降了，如图1.3所示，当$W_S=24,W_I=1$时，通带内的量化噪声衰减约为$-12dB$，有效降低了量化带来的噪声影响，尤其是在大功率的情况下，能够实现无差错传输，而如果使用普通的量化方案，在高接收光功率的情况下仍然不可避免地存在一些错误。

加权矩阵对FIR滤波器噪声整形的影响

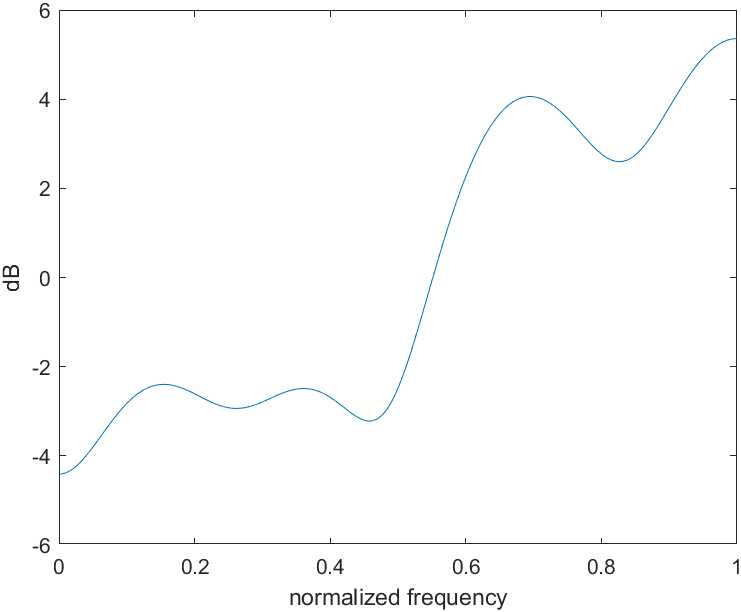
在上面的讨论中，噪声整形时使用的加权矩阵为$W_S=24,W_I=1$，若取$W_S=2,W_I=1$，不满足$W_S \gg W_I$，得到的幅频响应曲线如图3.3所示，可以看见其通带内的衰减较小，且起伏较大。

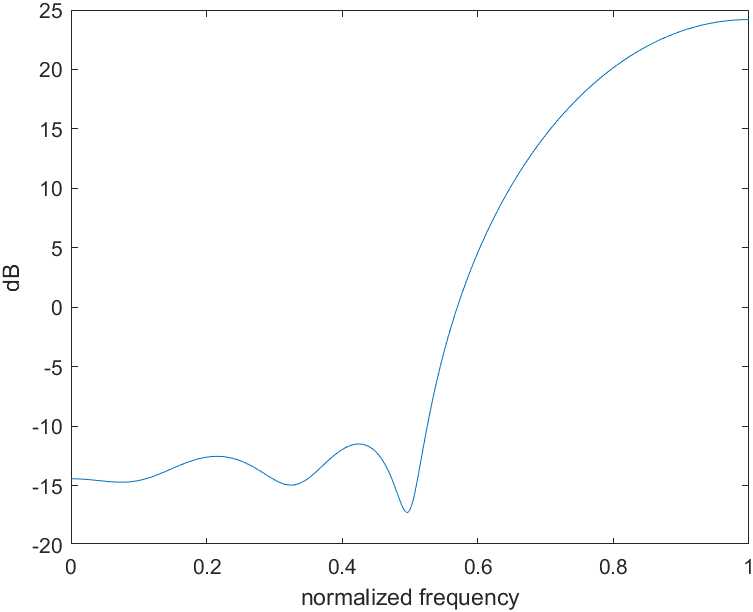
若取$W_S=50,W_I=1$，得到的幅频相应如图3.4所示，可以看到，其通带内的衰减更大了，达到了$-15dB$，与之相对应的，信号带外的噪声分量更大了。

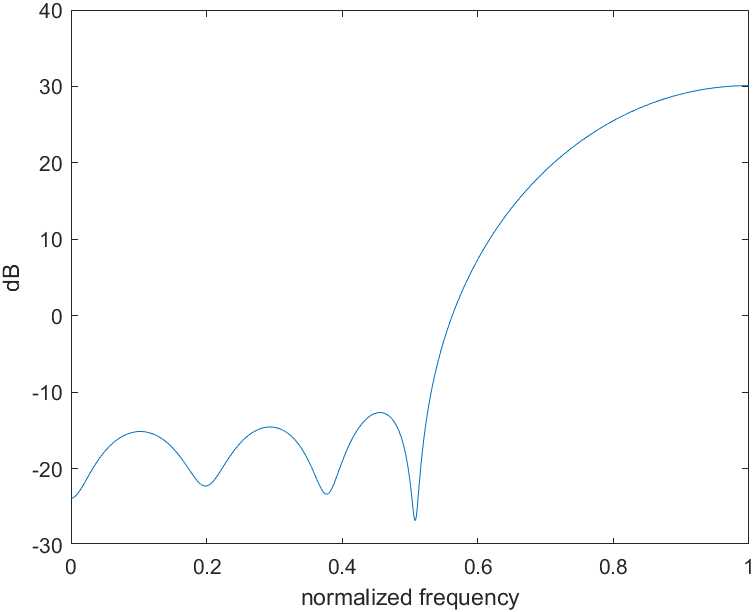
那么是否增大$W_S$就可以得到性能更好的幅频相应输出呢，如果将加权系数设为$W_S=500,W_I=1$，幅频相应如图3.5所示。可以看到，此时的信号带内衰减并没有继续增加，相反起伏更大了，这就意味着不能通过无限地增加$W_S$来获得更好的性能。

在上述讨论中，FIR滤波器的阶数均为七阶，如果增大滤波器阶数，得到的幅频响应如图3.6所示，可以看到其信号带内更加平缓，但是相对地，吉布斯效应也就更加明显。

相反，如果降低FIR滤波器的阶数，如图3.7，得到的幅频响应则不能很好地实现信号带内的噪声抑制。